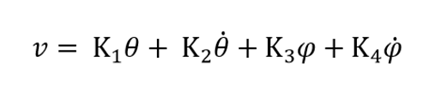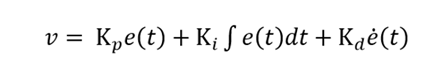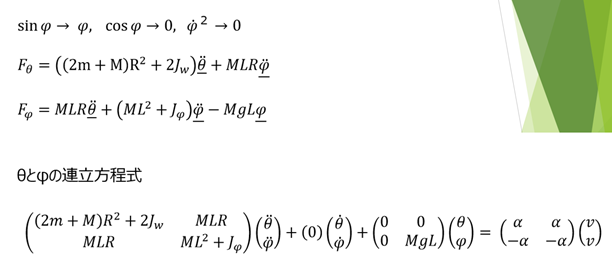F# Advent Calendar 2015 – connpass の 12日目です。
中身的には 倒立振子ロボットを MonoBrick で作成する(F#編) | Moonmile Solutions Blog の延長線上で、何故 F#(関数型言語)でロボット制御をやろうとするのか?ってのをつらつらと書いていきます。
C# 版は、EV3 + MonoBrick + C# なスライドを参照して貰うということで、計算のところを少し突っ込んで行きます。
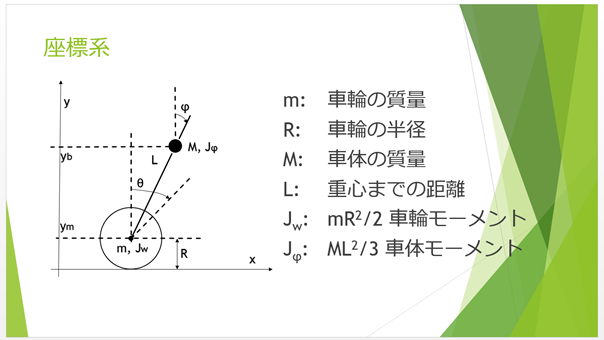
物理方程式を解く
実は、制御工学を習ったことが無かったので知らなかったのですが、倒立振子ロボットのように「状態の変化に対して少しずつ対応していく」という方式は単純な線形の式で表せます。線形と非線形の違いは、直線近似とそれ以外の複雑な変化を解くという違いにもなりますが、ある意味で物理現象のような「とある時刻 t の状態から、少し異なった t+Δt の状態を予測する」という場合には、線形に近似をしても問題はありません。Δt のサンプリング周期にも依りますが、とある複雑な予測解析を行う場合は、未来の t’ の値を直接計算するよりも Δt の積み重ねのほうが簡単に計算できたりします。
これは、よくやる重力の物理方程式で、惑星の動きとかをシミュレーションするときによく使われる方法ですね。太陽と地球の場合は、楕円として計算できるけど、三体問題として太陽・地球・月の場合は複雑に絡み合っているので直接計算はできません。別途 Δt で計算するというアレです。
当然、Δt は近似であるので、その積み重ねによって計算された未来予測値は正しい値とは限らないし、むしろずれています。誤差が累積されますからね。しかし、制御工学のように、その時々の時刻 t’ の値を観測することによって、Δt による線形近似のずれは、その t’ 毎によって補正されるため直近の値のみ正確であればそれでよいのです。このあたりを踏まえると、倒立振子ロボットのように一見、実現不可能ようなもの(私自身が倒立振子ロボットを見たのは、つくば博覧会のときですから30年以上前です。そのときに出品していた、一本足ロボットが現在の iRobo の前身なのですから驚きですね)であっても、意外と簡単な近似だけで行けるものです。
上記の運動方程式をあれこれラグランジュ方程式で解いて、変換すると、
角度θ、φに対するゲインの式
予測値に円滑に近づけるための PID 制御
の 2つだけで十分なのです。
それぞれの定数(K1, k2 等)を決めるためには複雑な方程式を解かないければいけませんが、最終的に倒立振子ロボットを制御するためのロジックは、上記のような単純な式であらわせます。これが組込みで動くので、Arduino のようなメモリが少ないマイコンでも動くという仕組みです。
科学計算の式をプログラム言語で解く難しさ
ここで注目したのは、最終的な式は簡単に見えるけども、途中の計算は複雑だということです。それぞれの K1 のような定数は、既知の数値のように見えますが、ロボットの重心位置や質量、タイヤの半径や質量、モーターの角速度や逆電流などに関わってくる定数になります。このあたり、科学計算の式をプログラム言語に直すときのむずかしさがあり、その間はギャップがあります。
- 数式として解いたときの式
- プログラムコードで実現するコード
の間には結構な隔たりがあります。
このような式を、プログラム言語(C言語や、C++、C#,Fortran など)に直していくわけですが、これがなかなか大変です。書き直すときのコツもあるのですが、問題は「式」の表現と「コード」の表現に大きな隔たりがあることです。
仕事上、数式を Fortran、C++ で書き直すことをやっていますが、よく間違えます。ただし、数式として抱えている様々な条件(前提条件なども含む)を写し間違えるあわけですね。その間違い、実際もとの数式に当てはめないとわからなかったり、複数の式が絡み合っているとなかなか見つかりません。
そんな仕事の中でよく使っているのは、F# による検算です。
- 数式を書く(与えられる)
- F# で書く
- C++、Fortran で書き直す。
- 3 と 2 の答え合わせを xUnit で行う。
という方法をよくやります。これをやると数式の写し間違えが激減しました。理由は F# が関数型言語で、式の取り扱いが得意だからというのもあるのでしょうが、検算することにより不具合率が減ります。また、この F# で書くコードは、巷の関数型言語特有の複雑さ(モナドとかオプショナルとか)をまったく使わず、ごく普通に式をプログラム言語に直す、というスタイルでしか使っていません。ですが、不具合が激減します。
束縛(バインド)と関数内関数の活用
ここ 2 年間の経験上ではありますが、この不具合率の低さは、
- 束縛(let)の利用により、できるだけ値を不変にしようとする努力をする
→ 影響範囲が少なくなる - その場でしか使わない関数は、関数内関数として定義する。
→ 関数名が短くて済む。影響範囲が狭い。 - if文、switch/match 文が値を持つ
→ 型システムの利用
なところです。
値の束縛は、C言語であれば define 定義すればよいし、C# であれば const にすれば ok です。ですが、F# の場合(関数型言語一般)は、デフォルトが束縛(let)であって、値を変えたいときはわざわざ、mutable にしないといけないという面倒臭さがあります。これが「面倒くさい」ことによって、より値が変化しない束縛(let)のほうにコードが寄ってきて、影響範囲の少ないコードが書きやすくなるという利点が出てきます。
逆に言えば、オブジェクトのプロパティをがりがりと変化させるようなオブジェクト指向とは別の向きを関数型言語は示してくれます。それは相反するものではなくて、その場その場でより使いやすい方向に向ければよいので、オブジェクト指向も関数型言語も相補的な形で使えるでしょう。
そういった場合、倒立振子ロボットのような物理的な制御をする場合には、物理量が不変であるからこそ数式的に関数型言語を使う法が適しているといえます。逆にロボット制御であっても、リモートコントローラーでアクチュエーター(サーボモーターやアームなど)を適切に動かすような主導的な制御はオブジェクト指向/UML を使ったほうがうまく作れるとも言えます。そういうパターンを踏まえて、物理値を逐次観測していてアジャイル的に制御を加えていく制御工学な自立コントロールはなかなか面白い分野になります。
サンプルコード
倒立振子ロボットを F# で書いたコードです。
moonmile/MonoBalancer
https://github.com/moonmile/MonoBalancer
C# と見比べると面白いかも…というか、今は C# から F# に書き直しただけなので、そのうち F# らしいスタイルに直していきましょう。