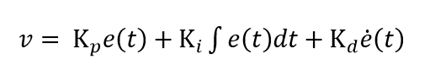11月の.NETラボ勉強会で発表した倒立振子ロボットの補足です。
EV3 + MonoBrick + C#
http://www.slideshare.net/moonmile/ev3-monobrick-c
実は、制御工学の話からプロジェクト管理とかアジャイルとかテスト技法に繋げてみたかったのですが、話し忘れました。私自身は工学部出身なのですが、制御工学は習わずじまいだったんですよね。電磁気学とか量子力学のところは通っているので座標変換まわりは大丈夫なのですが、一番の驚きは時間軸の t の項を式に加えるというところです。
以下は雑多な話として、かつ既に制御工学/品質工学の専門の方には当たり前のことかもしませんが、ちょっと比較として面白かったのでメモ的に残しておきます。
制御工学はハンドリングの技術
ハンドリング、フィードバックは、アジャイルプロセスやプロジェクト管理の世界ではよく聞かれる用語です。その元ネタは、制御工学にあると知ってはいたものの、そのままの言葉とそのままの手法が制御工学の中にある(当たり前といえば当たり前)のちょっと吃驚です。制御工学の教科書として「はじめての制御工学」「はじめての現代制御理論」の本を使っているわけですが、一番わかりやすい制御のたとえとしては、車のハンドリングがあります。人が車を運転するときに少し左にずれれば少し右に、少し右にずれれば左にと小刻みにハンドルを動かします。この「ハンドリング」は当たり前といえば当たり前ですが、初期値のハンドルを決めた後、ずっとそのままではなくて、途中でハンドルをちょこちょこと動かすわけです。たとえ、直線の道であっても道の凸凹や車の揺れなをを修正しながらまっすく走るように制御をします。
ちょうど同じ例えば、アジャイル技法にもあって、プロジェクトを進めるときには途中途中でハンドリングをするたとえ話が出てきます。最初に決めた仕様や設計に従って、まっすくぐに進むのではなくて、途中途中の動きに合わせてちょっとずつ目的に向かうように修正していく手法です。ウォーターフォールの管理(本当のウォーターフォール技法ではなく、一般的に知られている/嫌われている「ウォーターフォール」の方)では、最初の仕様/設計に従って突き進みます。つまり、最初の角度に従って真っすぐに進むという方法ですね。そうなると、ウォーターフォール管理に「制御」があるかというと、制御はありません。途中途中でみられるものは単なる「観測」であって、観測を本線の制御にフィードバックする仕組みがありません。また、アーンドバリューは予測にはなりますが、予測をした後にどうするか?の基準がありません(現在の価値の傾きからどのくらいの遅れが発生するのか?という予測は立てられます)。どちらにせよ、出発時点で方向を変えないのであれば、制御ではありません。厳密にいえば、初期値=時間が0 のときだけ考慮するので、制御工学の大切な t の項が出てこないためです。
そんなわけで、制御工学を IT のプロセス管理/改善に含めるためには、必ず時間軸の t 項が必要になってきます。
理想状態では制御がいらない
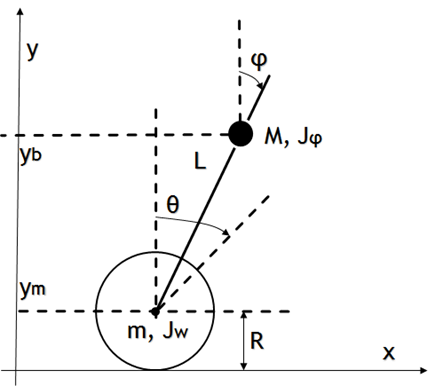
これは、倒立振子の座標軸を示したものですが、完全な倒立状態の場合には、θとφは0になります。倒立状態のときに、これまた理想的な状態の場合は、完全な倒立が成立した後は永遠に倒立します。理想的な棒と理想的なタイヤが、理想的な倒立をした場合には永遠に倒立するであろうことは容易に想像できますが、それは「理想」でしかなくて、現実的なところは必ずすぐに倒れます。何故でしょう?
倒立のために理想的な初期値を与えたときは、時間軸の t の項に対する変数は常に変化が 0 になります。永遠に倒立しているのだから、θもφも 0 のままですよね。しかし、現実には時間 t によって変化をするので、θ(t) と φ(t) になります。t に依存するわけですね。ここで面白いのは、
- t = 0 のときに初期値が 0 ではない。
- t > 0 のときに初期値とは異なる値になる。
という 2点があります。t = 0 の場合は、まさしく初期状態で、倒立振子ロボットを最初に手で立たせようというところです。また、壁に倒立振子ロボットを寄りかからせて立っているところを想像してください。どちらにせよ、θ = 0 に近い値がいいのですが、現実問題として 0 にはなりません。なんらかの揺れが発生するわけです。かつ、時間が進んで t > 0 の状態では、なんらかの要因で θ の値は刻々と変わります。それは倒れる瞬間かもしないし、ゆらゆらと制御しながら立っている瞬間かもしれません。少なくとも t > 0 の時点では、θ と φ は一定ではない状態が続きます。
これもプロジェクト管理やアジャイルプロセスと同じで、初期の状態はどうやっても理想形にはなりません。むしろ理想形にはならないという前提に立つことが、制御工学からわかります。また、時間が進みに従って、いろいろな要因がかかわってプロジェクト内の設計や要件が揺れるわけですが、これも t > 0 の条件にあたります。初期値は理想的ではないし、途中の進捗率も理想的にはならないのだから、なんらかの制御が必要になりますよね。逆に言えば、理想的なプロジェクトでは制御なり管理(マネージメント)は必要ありません。ですが、現実は理想ではないので、なんらかのマネージメントが必須になります。
フィードバック制御の効果は遅れてやってくる
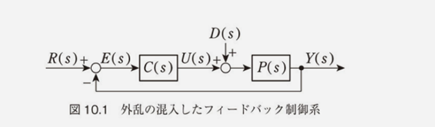
制御工学ではブロック線図が使われます。音響関係やコイル/コンデンサを使った発振も、このブロック線図を書いてフィードバックの向きを入れます。
このフィードバックですが、オブジェクト指向的には一瞬で終わる( t の項目がない)ように見えますが、実はフィードバックは遅れてやってきます。この図はラプラス変換されたものですが、目標値とのずれをC(s)で制御として記述し、それに外乱要因が D(s) として追加された後、操作を P(s) で行います。これが時間の項目がないと、オブジェクト指向的に一瞬で計算が収束する Δt = 0 となるわけですが、実際にはΔt > 0 になります。このために時間軸が発生して、
こんな感じで、時間軸のそれぞれの出力値 y(t) が変わってくるわけです。オブジェクト指向やアスペクト指向自体も、遠地のメッセージングやネットワーク環境などを考えると t の項目が出てきます。それが複数のスレッドの場合は、遅延を考えたり、デットロックを考えたりする基準になるのですが、このあたりもオブジェクト指向と時間 t の関係を考えると色々と面白いです。
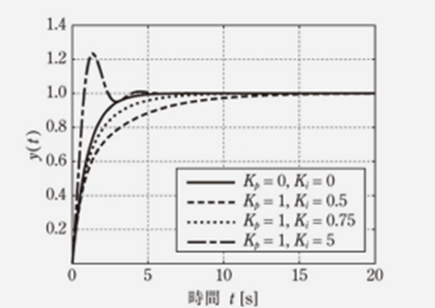
さて、最終的な出力からのフィードバックは、次の t にマイナス制御として働きます(なんらかの値へと収束させようとする力)。これをより安定的に制御するためには、グラフのように上に飛びぬけた「オーバーシュート」の状態では困る場合があります。また、なかなか収束せずにゆらゆらと振動してしまう場合も困ります。
これを安定稼働させるために PID 制御があって、それぞれ差分と積分と微分の項があります。
この Kp,Ki,Kd をうまく決めてやることによって(行列の状態方程式を解くことで値を計算できます…まだ私は計算できていませんが)、オーバーシュートをせず、振動が起こらずに目標値に着地させることができます。それぞれの項目が何を意味するのかは、最初の車のハンドリングの話に戻ります。地面の揺れや車の揺れに従って、時間 t に沿ってちょこちょことハンドルを動かして真っすぐ動かすようにします。しかし、大きくハンドルが外れた場合、大きく戻すと簡単にオーバーシュートしてしまいます。ハンドルが切りすぎの状態になって蛇行してしまいますよね。大きくハンドルが外れた場合、あるいは大きく曲がる場合は、少しずつハンドルの向きを調節して、最終的に大きなずれをなくすようなハンドリングの仕方をします。当たり前といえば当たり前の動作ですが、これをプロジェクト管理に当てはめてみましょう。
何らかの大きなトラブルがあって、プロジェクトの進捗が大きく遅れたとします。1日がっつりと進捗が遅れた場合はどうすればいいのか?ってことですね。1日遅れたのだから、プロジェクトメンバを休日出勤させて1日取り戻してはどうか?というのが、よく使われる進捗管理の方法だと思うのですが、どうでしょうか。制御工学的には、大きなずれは少しずつの制御を積み重ねたほうが、オーバーシュートや振動が少なくなるわけです。ならば、プロジェクトの進捗が大きく遅れた場合に、1日の休日出勤を行ってはダメですよね。オーバーシュートが起こりそうです。そうなると、遅れはちょっとずつ取り戻したほうがよいのではないか、というのが制御工学的な考え方です。
制御がうまくいかなくて、元の値の上下を振動してしまうのは、元に戻す力が早すぎる(たいていは加速度のゲインが大きすぎる)ことです。これを、ゆるゆるとやるのが制御の基本です。何故、少しゆるくやるのかというと、フィードバックの効果は遅れてやってくるからです。これは、RC 回路の高周波のフィルタでも同じで、少し遅れるために振幅が相殺されてしまう現象と同じです。となれば、物理現象をプロジェクト管理に応用すれば、なんらかの対策を打ったとしてもその効果があらわれるのは少しあとになりますよね。大抵の場合は、すぐに効果が表れると思って(期待してしまって)なんらかの効果が出るものに執着したり、効果がでないとすぐに別の対策を立てたりしますが、実はフィードバック効果自体は少し遅れてくるのが物理現象なのです。ならば、ならかの対策を打ったときには対策の効果がでるまで、時間が掛かることを知って対策を打ちましょうということです。
フィードフォワードで予見する
倒立振子ロボットのプレゼン資料には「フィードフォワード」の話はできません。フィードフォワードは、フィードバックの逆で、先に手を打つことです。先に書いた通り、フィードバック制御だけでは、効果が遅れて発生するので常に後手後手の制御になってしまいます。ならば、目標値に沿うように、外乱の要因をあらかじめ低減するのがフィードフォワード制御の役目です。外乱ってのは何かというと、予期しない揺れみたいなものですね。ですが、外部からの揺れであっても一定の法則があってり、一定の範囲で測定できたりするわけで、その項目が過敏に働かないように制御を入れることができます。
まだ学習途中なのですが、フィードフォワード制御を使って外乱に過敏にしないようにするためには、多変量解析の仕組みを利用して、加味する値の影響度(ゲイン)を調べるといいでしょう。余分な雑音を雑音とみなすために、影響度を小さくします。これはちょうど、数式の中に sin θ を θ が微小のときには sin θ ≒ θ とみなす、ことと似ています。より小さくなる自乗の項目を減らしたり、局値を取ったりして式を簡単にして解きやすくします。
じゃあ、これがプロジェクト管理の場合にはどれに対応するのだろうと考えてみると、ちょうどスクラムプロセスのスクラムマスターの役割に似ています。プロジェクト内のエンジニアが外部の雑音(金額交渉やスケジュール交渉など)に惑わされないよに防壁に役割をします。雑音を雑音と扱い、重要なものだけ通すフィルターの役割をする分けですね。
また、常に対策が後手後手になってしまうフィードバック制御(「進捗どうですか?」など)ではなくて、何らかの予測のものに先手を打つことが必要です。マイルストーンを置いたり、バーンダウンチャートで不具合の収束度を見極めたり、増員をしたりという早期対策ですね。
このあたり、色々考えながら制御工学の式を解いています。最終的には、いくつかの固定値と簡単な足し算の式だけで、倒立振子ロボットが倒れないで済むのが驚きです。簡単な式だからこそ、マイコンとしてメモリの少ないチップでも十分制御ができるしアセンブラで書くこともできる(まあ、そのほかの動作がややこしいんですが)のですね。このあたり、サーボモータも PID 制御をしていて面白いです(というか、サーボというのがその制御そのもの名前だった)。
このあたり、本格的な制御工学とプロジェクト管理/アジャイルプロセスが、どう組み合わさるのかは考えてみたいところです。少なくとも、私にとって制御工学というジャンルはそういう目でも見ています。