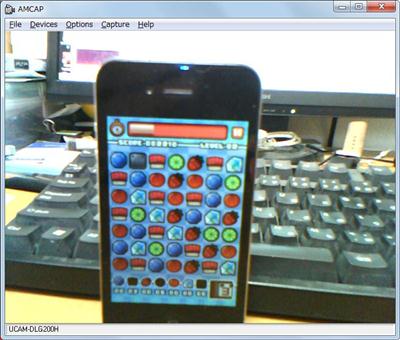
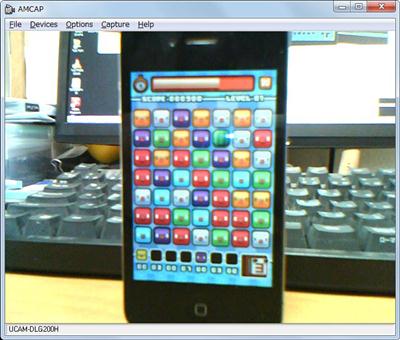
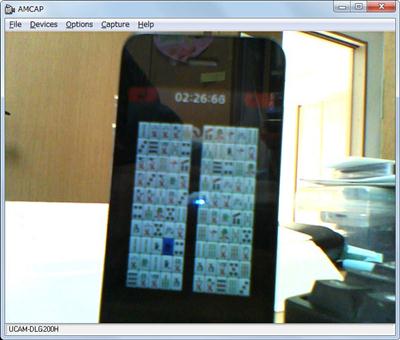
テンプレートマッチング法を使うと、教師画像を実画像から簡単に検索できるのだが、相関係数（CV_TM_CCOEFF_NORMED）を使って探索をすると結構遅い…というか、これが目で駒を追うやり方なのかどうかが疑問だったりします。
なので、以下は、ちょっと考察。
なにも、教師画像のすべてをマッチングさせる必要はなくて、教師画像の特徴を掴んで、実画像とマッチングさせればよいのです。これを特徴量という言い方をするのですが、この特徴量の定義として考えられるのが、
- 教師画像の、色で検出する。
- 教師画像の、形で検出する。
- 教師画像の、白黒画像で検出する。
- 教師画像の、角で検出する。
というやり方があります。
画像処理 (3) 顕著性マップ
http://fussy.web.fc2.com/algo/algo12-3.htm
をつらつらと読んで考えたのが、教師画像での顕著性のある場所が、実画像のマッチングする枠と比較してどうなのか？ということで、教師画像の特徴を掴むという行為は、実は、「色」だったり「形」だったり、「白黒」画像の「白」の位置だったり、「角」っこであったりするわけです。そう、「あったり」する訳なので、実は、それぞれの場面によって異なるのが普通ではないかと。
そうなると、教師画像を１枚だけ見て、どこに特徴があるのか？という行為／計算では足りなくて、実は、
- 複数の教師画像から、それぞれの相違のある箇所（＝特徴量）を見出す。
- 教師画像と実画像をいくつか比較して、正解しやすい特徴量を学習する。
というパターンになります。
で、このどちらのパターンであっても、特徴量を検出する場合には、色／形状／輝度／角などの検出を決め打ちするのではなくて、その場面によって（実画像からどのような教師画像を見つけるのかなど）、特徴量の検出パターンをどれかに決めるという手順が必要ではないかと。
例えば、今、手元で実験している３マッチのアクションパズルは、果物を使っているので形状でも認識できそうですが、ちょっと前のバージョンでは形状が全く同じなので、色でしか判別できません。
また、二角取りのように麻雀パイを使う場合には、マッチングの分類を「萬子」「索子」「筒子」「その他」に分けて検出しないとスピードが上がりません。と、言いますかマッチングパズルをしているときに、そういう見方を私はしています。
なので、画像をマッチングで検出する場合には、
- 教師画像の特徴を検出する（色、形、輝度、角など）。
- 教師画像の特徴点を決定する（背景画像の除去、不必要なノイズは検出させない）
- 教師画像同士で、1,2 が妥当であるか検証する
という前処理があった後
- 初回は、実画像の全箇所をテンプレートマッチする？
- 次回以降は、前回の箇所から探索をする。
- 検出箇所を、教師画像と再検証させる。
あるいは、ランダムにマッチング箇所を決定する？
あるいは、顕著性マップなどから、注目点と特定する？
見つからない場合は、4 に戻る。
という探索が必要になるのかなと。
実画像（検索の対象画像）をランダムに検索しようとするのは、目的が動画（リアルタイム）からのピックアップにあるので、実画像からの駒の検出は、計算時間を 30fps の間に収めたいわけです。時間にすると 33 msec というところですね。
この短い間に計算を終えるためには、あらかじめ、検出すべき特徴を頭に叩き込んでおいて実画像から素早くピックアップしなければいけません。例えるならば、サッカー選手が首を振った瞬間に、チームカラーで味方と敵の選手の位置を把握するようなものです。なので、あらかじめ教師画像から特徴量を決めておき、検出する箇所も数か所から数十か所に絞り込んでおいて、実画像とマッチングさせます。この場合、誤検出は出るでしょうが、それは 6 の再検出あるいは、特徴自体を数種類で取り込むことで検出率を上げるようにします（検出率を上げるという確率の方法を取り、100% の完全性は求めないところがミソです）。
で、そんなこんなで、特徴箇所だけでマッチングをするためには、cv::matchTemplate 関数にマスク値か探索位置を渡す必要があるので、コードを改造するしかないのかなぁ、と思ってソースを追っていたところ。
templmatch.cpp の 235 行目から cv::matchTemplate 関数の記述があって、sum 部分は 269 行目から、2 次元の繰り返し部分は、318 行目からになっているので、それなりに改造できそうかなと。
for( i = 0; i < result.rows; i++ )
{
float* rrow = (float*)(result.data + i*result.step);
int idx = i * sumstep;
int idx2 = i * sqstep;
for( j = 0; j < result.cols; j++, idx += cn, idx2 += cn )
{
// ここで mask を渡しておいて、
// if ( mask(i,j) == 0 ) continue ;
// のように skip させれば ok ?
// 加えて、sum を計算しているところも mask を見るように修正？
double num = rrow[j], t;
double wndMean2 = 0, wndSum2 = 0;
if( numType == 1 )
{
// CV_TM_CCOEFF CV_TM_CCOEFF_NORMED のループ
for( k = 0; k < cn; k++ )
{
t = p0[idx+k] - p1[idx+k] - p2[idx+k] + p3[idx+k];
wndMean2 += CV_SQR(t);
num -= t*templMean[k];
}
wndMean2 *= invArea;
}
if( isNormed || numType == 2 )
{
for( k = 0; k < cn; k++ )
{
t = q0[idx2+k] - q1[idx2+k] - q2[idx2+k] + q3[idx2+k];
wndSum2 += t;
}
if( numType == 2 )
num = wndSum2 - 2*num + templSum2;
}
if( isNormed )
{
// CV_TM_CCOEFF_NORMED の箇所
t = sqrt(MAX(wndSum2 - wndMean2,0))*templNorm;
if( fabs(num) < t )
num /= t;
else if( fabs(num) < t*1.125 )
num = num > 0 ? 1 : -1;
else
num = method != CV_TM_SQDIFF_NORMED ? 0 : 1;
}
rrow[j] = (float)num;
}
}
これを流用してマスク画像を渡す方式にするのか、x,y 座標を含めた 1 次元配列を渡すのがよいのか、思案中。
2 次元の mask を取るほうが楽みたいだが。
