コードの品質は、コードの不具合を直すよりも、優先度が高いのだッ!!! … というのを、数式で証明するテストです。
数式というか、シミュレーションですね。プログラミングをするときの不具合の混入率と不具合の修正日数を変数に入れれば、おおまかにコードの完了予定日が計算できればよいかなと。
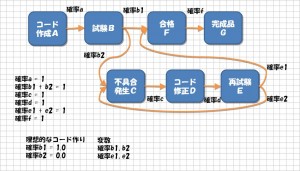
まずは、状態遷移のモデルを作ります。
状態と作業タスクが、多少ごっちゃになっていますが、
A.コード生成
B.試験
C.不具合発生
D.コード修正
E.再試験
F.合格
G.完成品
という具合です。
ある状態からある状態に移るときに、確率を利用します。必ず次の状態に移るときは「1.0」という具合。
確率の部分を除くと、PERT 図と同じになるので、それぞの状態≒タスクになります。
「合格」や「不具合発生」の場合は、実は現象をあらわすだけので、作業日数は「0.0」とすれば OK です。まぁ、このあたりはおおまかに。
システムダイナミクスの理論を応用する…というか、フィードバックを入れるので、数式で解くよりも適当なプログラミングを行ってシミュレーションするほうが楽になります。というのも、このくらいのフィードバックと変数ならば数式でやってもよいのですが、このタスクをこなす【人員】の問題を入れると途端に難しくなるので、シミュレーションにします。
【人員】の問題というのは、試験、コード修正などを1名で行う場合には、単純な作業日数の累積になるのですが、実際のように複数名で行う場合、コーディングをする人と試験を行う人が違うとか、3名がコーディングと試験の両方をこなして手が空いた人が不具合を修正するとか、というような「待ち行列」の問題(サプライチェーンの問題ともイコールです)が入ってくるので、単純にはいきません。いわゆる「M/M/N」の待ち行列になるわけです。
あと、状態遷移図を見ると分かるとおり、非常に低い確率ではありますが、不具合修正が不具合を呼ぶというループがあります。この事象を適当な回数で切り捨てるために(確率が低いので)、「試験完了まで80%で終わる確率の日数は、何日か?」というような、答えを確率で計算する場合も数式だけだとちょっと難しいのです。まぁ、実際に応用するためにも、厳密な計算値よりも、大雑把ではあるがリスクの少ない数値(確度の高い数値)を拾っておいて、その他に関してはリスク管理として別立てにするとよい、ということころです。
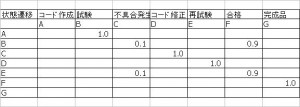
前置きが長くなってしまったのですが、状態遷移図を遷移表に直したのが次のものです。
[img 20111028_03.jpg]
遷移図と遷移表は同値なので、どちらかを使えば OK です。Excel で処理するには、遷移表のほうが便利かなと。
さて、これをどうやってシミュレーションしようかと考えていたのですが、オブジェクト指向的には、マルチエージェントシステム風に組んだほうがよかろうと思っています。この場合は簡単なものなので、専用のシステムは使わず、C# で組むか、Excel VBA で組むかというところですね。継承関係など複雑なものはいらないので、Excel VBA でも十分かもしれません。
という訳で、引き続き。