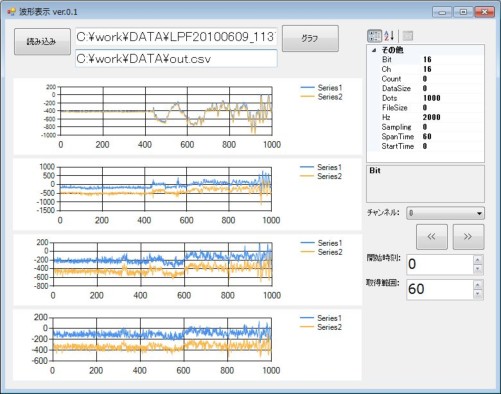
波形表示のサンプルソフトを作っている途中。
ちと、自分のメモとして。
- 周波数 2,000 Hz で、約1時間(3,600秒)ということなので、データ数は、7.2M のデータとなる。
- チャンネル数は 32ch 程度
このデータを、グラフで描画すると、ひどく大変。
データ数が 700万件なんて、まともに処理しようとすると専用のデータベースでも難しい。
のだが、ちょっとコツがあって、
- 描画するときには、ディスプレイの解像度が上限になる
というものがある。
つまり、横幅は、たかだか 1000ドット程度で十分な訳で、700万件を1000程度に集約すればよいわけだ。
ただ、
ここにも数学、という物理的なトリックを利用する必要があって(サンプリング理論ともいうけど)、
振動値を、普通にサンプリングしてしまう(間引いてしまう)と、本来必要なデータが欠損してしまう場合がある。
欠損というのは、
- 振動自体は、200Hz の範囲で変化する。
→ 0.1 秒の単位で注視が必要。
という条件がある。
言い換えれば、調べる目的というものがある。
それに沿っていえば、単純に間引いてしまうのは、ちょっとまずい。
200プロットの範囲で、どのくらいの重要なデータ(検出したい異常値)が現れるか、によってサンプリングの方法を工夫する必要がある。
なので、このような振動を検知する場合には、集約対象の範囲で、
- 単位範囲内の最大値を抽出してプロット
- 単位範囲内の最小値を抽出してプロット
というサンプリングをしないと、検出したい異常値が取れない。
そんな訳で、先の画像は、最大値と最小値をプロットしている、というわけ。
また、このような方法をとると、単純サンプリング(間引きの方法)とは異なり、集約範囲を自由に決めることができる。
ただし、これもダメな場合があって、
- 最小値、最大値で振動する場合、これの範囲で超えて、集約させてはいけない。
のですね。
このあたりは、理論になるので省略(気が向いたら、書きます、メモ的に)。
というわけで、この方法をとると、たかだかプロットするデータは1,000ドットになるので、データを集約する計算だけになります。
な訳で、結構なスピード(1秒以下)で、7.2Mのデータが処理できますね。
という話。