第7章の補足の続き。
実際のプロジェクトで計測してもよいのだが、実際のプロジェクトでは「同じプロジェクトは二度と発生しない」という1回性の制約がある。これはウォーターフォール開発でもアジャイル開発でも同じである。特殊な場合として「Wordpress を使ってホームページを量産する」ような工場生産のようなパターンもあるが、これはプロダクトの生産プロセスとして扱う方がよいだろう。つまりは手順化する&自動化するのが一番早いという形になる。
1回性のプロジェクトではあるが、毎度難解な試行錯誤を繰り返すのはプロジェクトメンバーの心理的な負担でもあり、毎回終わりのわからない未知のプロジェクトが発生するのはよくない。これは20年前以上から言われたことで「デスマーチ」というミームが使われている。
実験的に計画と実績を測定する
これをシミュレーション的に数百回繰り返せば、だいたい正規分布に従う結果がでるはず。というのを書籍でやりたかったのだが、ちょっと紙面が足りなかったのと、間に合わなかった。
ここで Excel を使って実験をしてみよう。
- 30個のチケットを作る
- 各チケットは3時間程度を目安にして、適当に散らばっている
- 実績時間は、やや遅れる傾向にある
という条件を付けてシミュレーションをしてみる。
マクロ付の Excel EVMと正規分布の解説.xlsm
ボックス・ミュラー法
チケットの予定時間や実績時間は正規分布で配置することと仮定している。これは後日証明することになるが、ひとまず、正規分布に従った予定時間や実績時間を計算するために「ボックス・ミュラー法」を使う。以下は、VBA のコードで、先のマクロ付きのシートに記述してある。
''' ボックス・ミュラー法
''' mean: 平均値
''' stdDev: 標準偏差
Function BoxMuller(mean As Double, stdDev As Double) As Double
Dim u1 As Double, u2 As Double
Dim z0 As Double, z1 As Double
Dim pi As Double
Dim i As Integer
Dim v As Double
pi = 3.14159265358979
' 0と1の間の乱数を生成
u1 = Rnd()
u2 = Rnd()
' ボックスミュラー変換
z0 = Sqr(-2 * Log(u1)) * Cos(2 * pi * u2)
z1 = Sqr(-2 * Log(u1)) * Sin(2 * pi * u2)
' 平均と標準偏差に基づいて調整
v = mean + z0 * stdDev
' 結果を返す
BoxMuller = v
End Function
平均と標準偏差を決めてチケットを作成
予定時間は、3時間を中心に標準偏差1時間で散らばることにする。書籍では3時間と決め打ちにしていまっているが、実際にはある程度チケットによって時間が変わるだろう。
予定時間に従って、実績が決まってくる。予定よりも早く終わることもあれば、予定よりも遅く終わることもある。大抵の場合、予測よりも遅くなることが多いので、4時間を平均値として標準偏差1時間で散らばることにする。もう少し正確な方法として、予定時間を平均値として標準偏差を1時間にするとよいのだが、ここでは思考実験なので数値を簡略化しておく。これを「実績」とする。
もう一つの列として「実績2」がある。これは書籍にあるように「タスクは予定よりも早く終わらない」原則を計算したものである。例えば、予定時間が3時間のときに、そのタスクが2時間で終わってしまったときに、残りの1時間をどう使うか?の問題である。大抵の場合、コードの品質を上げるために3時間まで使ってしまうか、休憩として使ってしまう。つまりは、予定3時間のタスクの実績は3時間以下になることはない、という想定である。これを「実績2」とする。
※後述するが、チケット駆動では、この余った時間を寄せ集めるように「チケットを前倒しにする」ことをでプロジェクトの納期を守る確率を上げるとができる。
これらをヒストグラムにする。
チケット数が30位ではうまいぐあいに正規分布にはならないが、おおむな3時間を中心にして前後に散らばっていることが解る。
また、実績では、中心が4時間となった同じ形のグラフになる。つまり、全体的に予定3時間が実績4時間に増えているわけで、1時間 x 30 チケット = 30時間の余裕をつければよい、ということが解る。
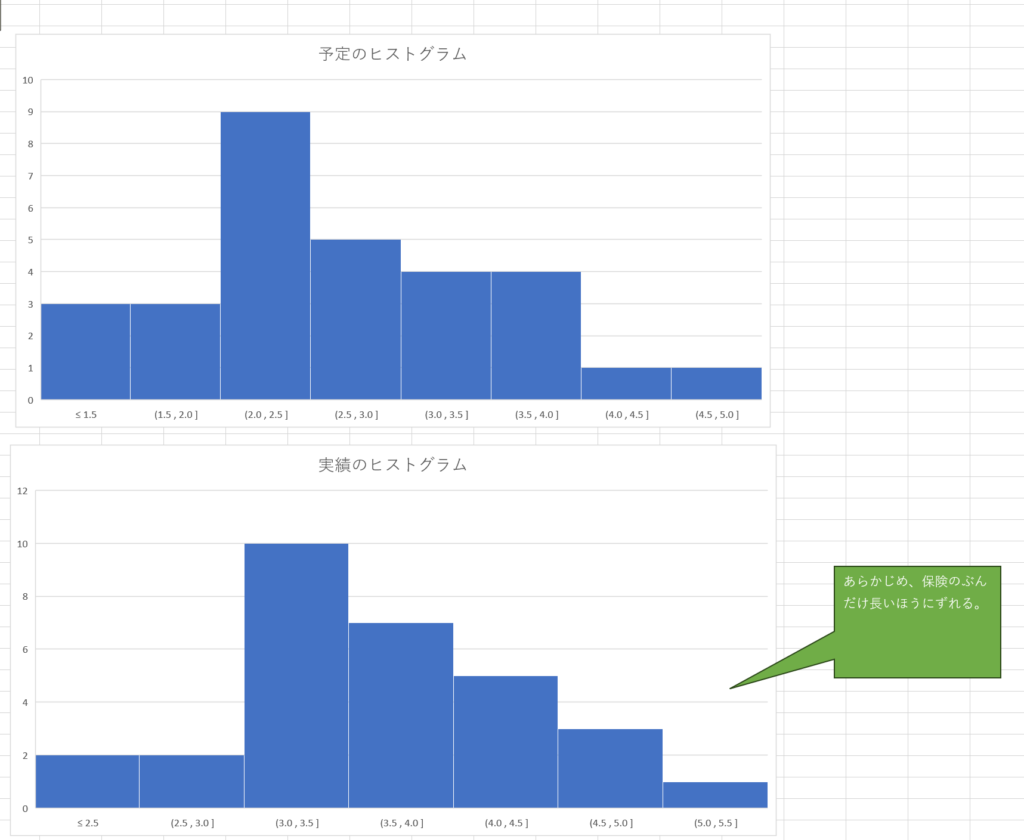
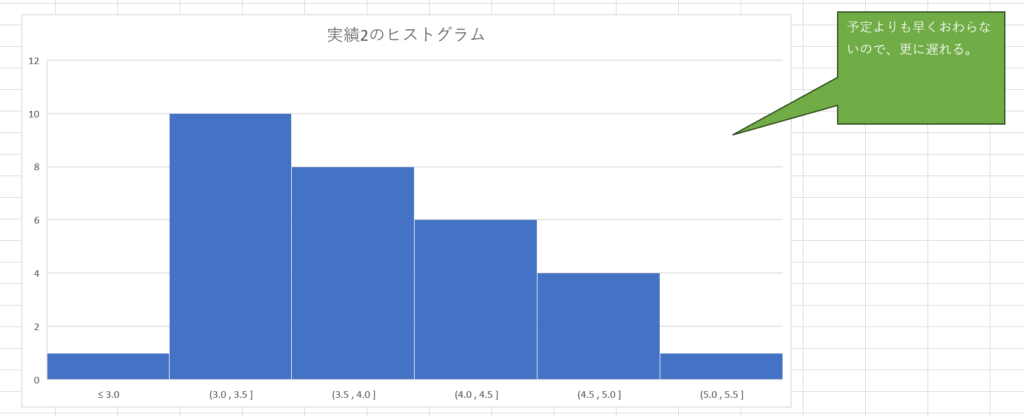
しかし、予定より早く終わることがない「実績2」のヒストグラムをみてみよう。
予定よりも早くおわることがないので、前者の「予定」と「実績」のグラフとは異なっている。ランダム値による計算なので、Excel を開くたびにかわってしまうのだが、予定に近い3時間の部分をピークとして、左側の3時間以下はほとんどなく、実績の4時間のほうに長いゆがんだグラフになる。これはもっと、チケット数を多くしてシミュレーションすると解ると思われる。
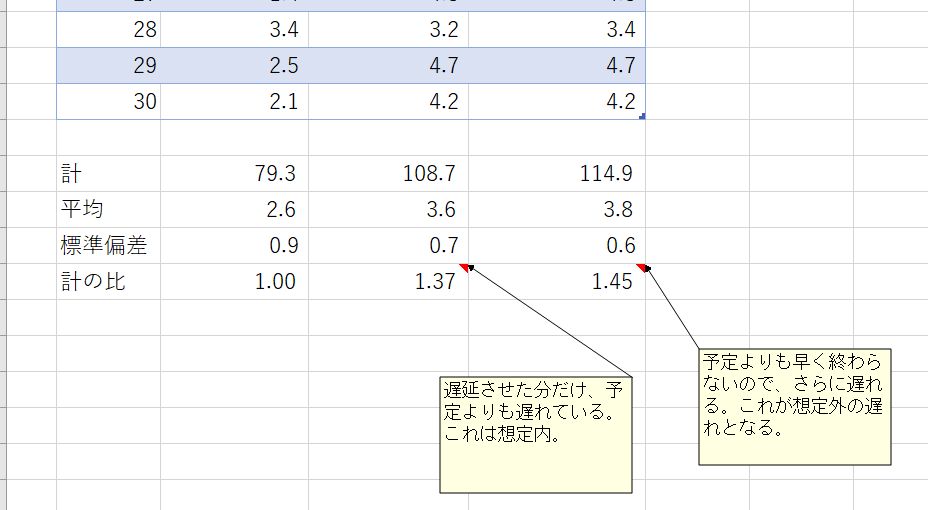
この実験の統計値をみてみよう(Excelシートでは、ランダム値を使わない「実験1」のシートがある)。
ランダム値なので、毎回計算値が変わってしまうが
- 計画時の合計 79.3時間
- 実績の合計 108.7時間(計画との差が約 30時間)
- 実績2の豪快 114.9時間(計画との差が約45時間)
という結果が得られる。
プロジェクト計画と実績との乖離は、要因として見積もりの甘さ(楽観的な規模見積)が伴うものが多く、これを回避するために保険(1.2倍や1.5倍など)をいれることもあるが、実際には、
- 計画から実績へのバラツキ(正規分布等)がある
- 実績は予定よりも短くなることはない
という理由があり、規模見積をしたときの保険自体の甘さも入ってくる。
ただし、これらの見積もりの甘さを複雑な計算式を使って正確に実績を予測することも可能おではあるのだが、あまり意味がない。というのも、開発を担っているのが人間である以上、「計画から遅れたら、残業してでも頑張る」という心理状態が働いてしまうからだ(あるいは、むしろ働かないほうを前提としたほうが期間見積はしやすい)。また、このシミュレーションでは複数のタスクをひたすら長い期間で対処できるのだが、実際の開発では1日の労働時間(8時間)に縛られるし、8時間の区切りでうまくタスクを調節しないといけない。それこそ会議や昼休憩などが挟まるので、思考のセットアップなどを含めると更に遅れることになり、測定値からずれることになる。ゆえに、正確な計算はあまり妥当ではなく、もっと大雑把な「方針」が求められる。方針を決めた上で、プロジェクトの着地地点(主にスケジュール)を立てることが求めらるだろう。
おまけ
なお、この現象は、WBSなどで区間をきっちりと区切ってしまうことによる弊害である。特に、きっちりと工程管理をされたウォーターフォール開発に多い弊害である。「きっちり管理」することにより、余計遅れるという現象である
チケット分割をして、「このチケットが終わったら、他のチケットも少し進めておこう」という、早めの着手ができる状態にしておくと解消される。これは書籍にも書いた方法である。


