感染症数理モデルでシミュレーションする（その１）

投稿日: 2020/02/29 作成者: masuda

板橋区は来週の火曜日から休校になります。各自いろいろな意見があるわけですが、そのあたり代理戦争はせず、「自衛」という一点でこれを書き留めておきます。
というかですね、「クラスター対策」の説明がされていないような気がするし、検査がなぜ行われないか（あるいは行うのか）、どういう形で決定したのかわからないのが問題だと思うんですよ。個人的に。なので、個人的に調べて、個人的にブログに書き残すという方針なので、そのあたりはご容赦ください。

詳しい情報をたどる

から

2019-nCoVについてのメモとリンク

にたどり着いたあとに「なぜクラスター対策が重要か」

のところまで来て、

Dispersion vs. Control

ここにたどり着きました。

中澤さんのページのリンクがある

①(02251430大臣レク用)クラスター班設置プレス

に「クラスター」の解説があります。これに基づいて厚生労働省は動いていると思われるのですが、そこはさておき、ここにでてくる「SEIRモデル」とは何ぞや？というところからスタートします。

SEIRモデル

SEIRモデル – Wikipedia

を見ると、比較的簡単な微分の方程式です。摂動論（古いけど）をやってた自分としては、ああ、となるし、機械学習を少しかじれば、ああ、となる式でしょう。それほど難しくありません。
時間tによって、状況が変化するという典型的な式です。

難しくはないんですが、いざ数式に直すとすると結構難しそうなので、先人の知恵を辿ります。

新型コロナウイルスの流行を科学的に考えるためのヒント｜ノルテ / 気象と波浪の研究者｜note

上記の記事から、SEIR の意味がこれです。

  • Susceptible: 感染症に対して免疫を持たない者（無免疫者）
  • Exposed: 感染症が潜伏期間中の者（感染者）
  • Infected: 発症者
  • Recovered: 感染症から回復して免疫を獲得した者（回復者）

wikipedia の式と違うのは、短期間なので、「mは出生率及び死亡率」のmを0とみなすことができるからです。

Dispersion vs. Control からたどった先には、github の R のコードがあります。

[GitHub – HopkinsIDD/nCoV-Sandbox]

あと WHO からのデータはここです。

Situation reports

記号の意味を把握すると、先のS,E,R,Iの初期値の他に

  • β: 感染率
  • lp: 潜伏期間
  • ip: 感染期間

が必要になります。

そのまま R で解けばいいんですが、R が不慣れなので別なのがないかと探します。

感染症数理モデル事始め　PythonによるSEIRモデルの概要とパラメータ推定入門 – Qiita

に python の実装があるので、そのまま流用します。

Python で SEIR モデルを動かす

python 自体も不慣れなので、コードとか変数とかはそのままなのですが、以下の3つをインストールした後に

pip install numpy
pip install scipy
pip install matplotlib

次のコードを実行します。

#include package
import numpy as np
from scipy.integrate import odeint
from scipy.optimize import minimize
import matplotlib.pyplot as plt

#define differencial equation of seir model
def seir_eq(v,t,beta,lp,ip):
    return [
        -beta*v[0]*v[2],
        beta*v[0]*v[2]-(1/lp)*v[1],
        (1/lp)*v[1]-(1/ip)*v[2],
        (1/ip)*v[2]]

#solve seir model
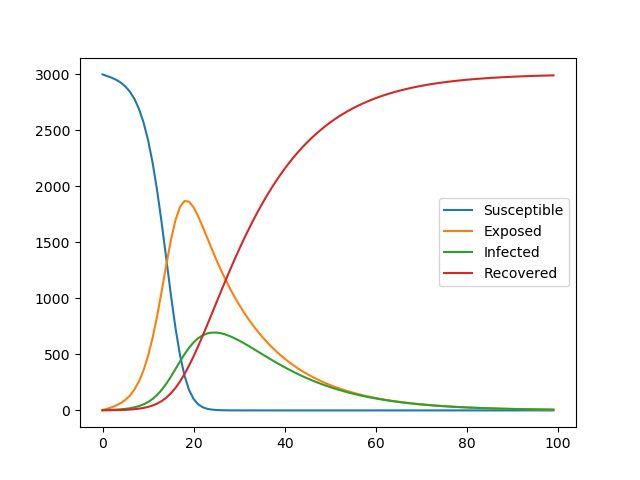
ini_state=[3000,0,5,0]
t_max=100
dt=1
t=np.arange(0,t_max,dt)
plt.plot(t,odeint(seir_eq,ini_state,t,args=(0.001,14,7)))

plt.legend(['Susceptible','Exposed','Infected','Recovered'])
plt.show()

パラメータの意味は、以下の通りです。

  • 初期S v[0]: 未感染者 3000
  • 初期E v[1]: 潜伏者 0
  • 初期I v[2]: 発症者 5
  • 初期R v[3]: 免疫獲得者 0
  • 感染率 beta : 0.001
  • 潜伏期間 lp : 14日
  • 発症期間 li : 7日

それっぽい数値を入れてみたのですが、あまり根拠はありません。実際は、それぞれの値は分布（分散）があるので、ランダム値でシミュレーションすることになるはずです。

意味合いとしては、閉鎖空間で3000人いたときに、初期状態で感染者が5人いたときの状況をしらべています。
感染率「0.001」の意味は、「基本再生算数：1人の感染者からうつる人数の目安となる」の R0（WHO で「1.4から2.5」）となるので

感染率 beta 
  = (初期感染者 * R0)/全体の人数
  = (5*1.4)/3000 = 0.0023

という計算となると思うんですが、よくわからないので適当にいれています。

追記:きちんと計算したものはこちら
http://www.moonmile.net/blog/archives/10384

感染率の分布を考える

実際は、感染率 beta や基本再生算数 R0 を推定するわけですが、現在のところ感染力ある程度推測されている（既存のインフルエンザよりも低い）ので、それを当てはめてみています。

ただし、インフルエンザ流行の「スーパースプレッダー」にあるように、感染はまんべんなく起こるわけではなく、とある閉鎖空間で一気に広がるであろうと想像されています。

となれば、感染率 beta には分布があるわけで、

  • とある空間では感染率 beta は限りなく 0 に近い
  • とある空間では感染率 beta は高い

というパターンになります。
今回、感染率の高い空間を「クラスター」と呼ぶわけで、それらは閉鎖空間であったり、不特定多数の人が密集している場であったりします。それらの「クラスター」同士をつなげないようにして、感染拡大を防ぐ、というのが「クラスター対策」の主旨ですね。

ひとまず「SEIRモデル」を数値計算してみたかったので、この後は感染率を分布（Θかσ）させるところへ。

カテゴリー: 開発 パーマリンク