下記のツイートをみて、ちょうど力学の解説によいと思ったのが落とし穴であった。ので、きちんとした解答を書き直し
「これが工学です」
Engineeringhttps://t.co/I1bfWq0iE6 pic.twitter.com/r4Qu19Jipa— ヤギの人(秋) (@yusai00) October 16, 2019
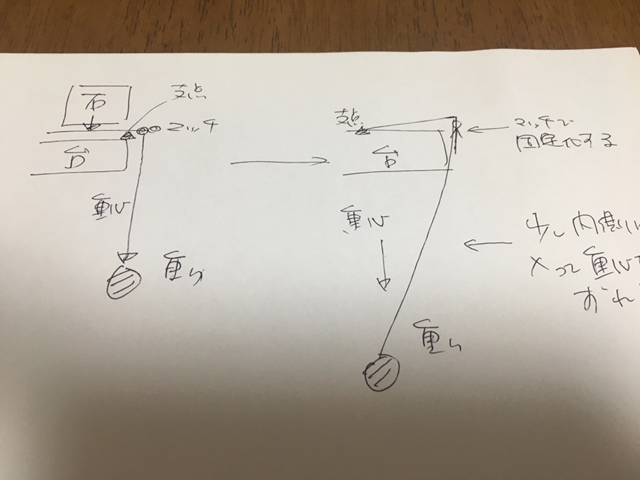
を見て思いついたのが、支点の移動の話で、下記な図を描いたのだが、これは間違い。
さきについていた、
先進科学塾@名大「遊びで探る重心の世界」2017.10.22 | ひろじの物理ブログ ミオくんとなんでも科学探究隊 https://ameblo.jp/hamgon1971/entry-12321955194.html
の補足で作ったつもりだったのだけど、上の図じゃなくて、こんな感じになる。
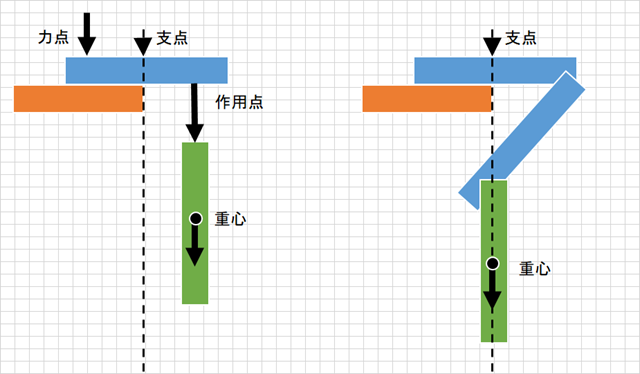
石で支えているときは、左のように重心が支点外側にあって力点を掛けてペットボトルを支えている。このまま石を外すと、作用点だけが残るのでペットボトルが落ちる。
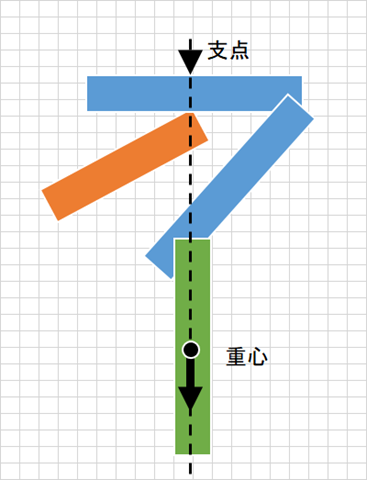
ここでマッチを使って左のように重心が支点の下に来るようにずらす。そうすると、支点の直下に重心が来る(支点自体が作用点である重心を支えるようになり、作用点=力点が等しくなる)、これによって、石がなくてもペットボトルは落ちずに支えられる、という仕組み
マッチの動画で「不思議」に見えるのは、ここの重心のずれ(支点への移動)がさりげなく行われるので、同じ格好でもペットボトルは落ちないという不思議さがうまれるのがミソ。
だから、極端な感じで先のブログにもあるように「指一本」で支えることも可能で、あらかじめ水色のマッチ棒の部分が固定化されていれば、一点で支えられる。
マッチ棒とゴムでは難しいので、実際に割りばしとビニール紐でやるとこんな感じになる。テーブルの上が平たいので左に落ちないので、やや浮いた形でバランスが取れる。下にぶらさがっている Linux ペンギンはちょうどテーブルの縁の真下に来る。
何処で勘違いしたのだろう
ミスリードになったところは、この部分で。
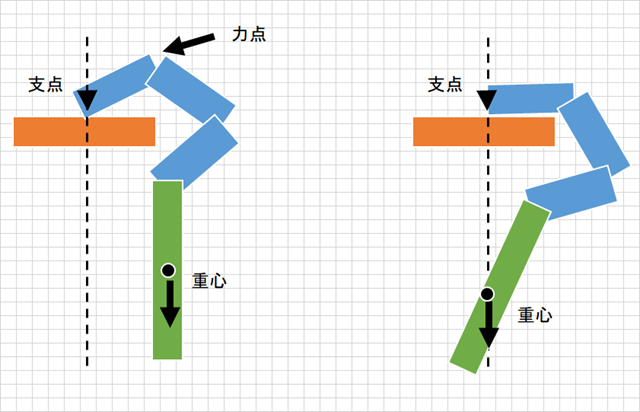
こんな風に取っ手のついた傘の動きを考える。
この場合、支点は傘の柄の先にあって無理矢理上から押さえつけて、傘の開くところを支えてまっすぐにしている。
これを手を離すと、傘の棒の部分が内側にずれて、重心が移動し支点の真下に来る、
ここに話を結び付けたかったのだけど、実は違ったということ。実は支点の先に(左側)に棒が続くかどうかの違いなんだけど、そこに引っかかってしまった、というか墓穴を掘った。うーむ。
材料工学的には片持ち梁の問題
この支点の問題なんだけど、材料工学では典型的な「片持ち梁」の問題だったりする。
片持ち梁とは?1分でわかる構造、様々な荷重による応力と例題 http://kentiku-kouzou.jp/struc-katamotiharitoha.html#targetText=%E7%89%87%E6%8C%81%E3%81%A1%E6%A2%81%E3%81%AF%E3%80%81%EF%BC%91,%E8%87%AA%E7%94%B1%E3%81%AB%E3%81%97%E3%81%9F%E6%A2%81%E3%81%A7%E3%81%99%E3%80%82
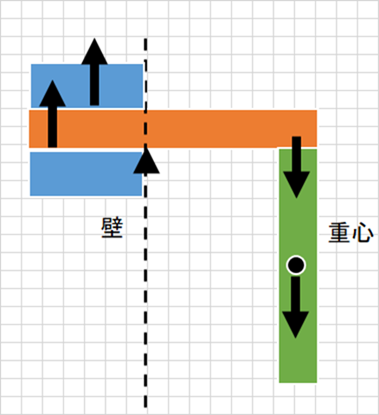
片持ち梁の場合、一方が固定点で片方が自由点。自由点のほうに何かをぶら下げると、応力かかるという問題。先のマッチ棒と傘の重心移動は、もういっぽうも自由点なのだが、ちょうどその中間を考えるとこんな図になる。
片持ち梁は壁に固定する(壁自体が剛体だから)のだが、釘みたいに壁に打ち込むタイプはこんな感じに力が働く。釘の上としたに力が働くわけで、接着剤の場合は下の面積(はがれる)が問題だし、コンクリート打ち込みの場合は上の力が問題(上がひび割れる)になる。
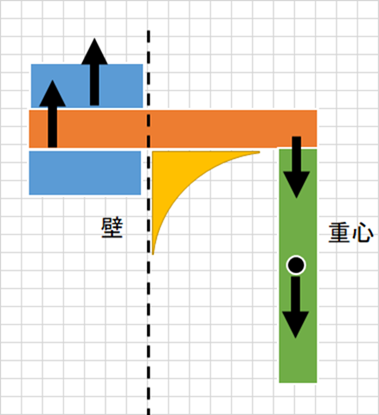
また、中間となる支点に大きな力が掛かるので、ここがひび割れる。支点のひび割れに対しては力を分散するために梁を使うか、R を付ける。この R 部分がおもしろくて、こんな風に黄色の部分を余分につける。
片持ち梁でもそうなんだが、この直角の部分の角には応力集中が働くので R を付けて応力分散をする、さらに支えともなる。という面白い特性がでてくる。
さらに先の「量産~」でツインドリル制作の時に聞いたのだけど、プラモデルのような場合でも同じように応力集中が掛かるので、こわれないように R を付ける。この R は、さきの棚のような場合には後付けになるのだが、プラモデルの型抜きのようなものは、金型のほうを「削る」という後から加工でいけるという特性がある。金属の型って、一発でできることは少なくて、少しずつ削っていくのだが、
- 金属の型のほうを削ると、材料のほうの厚みが増して強度があがる(安全性があがる)
- 最初は直角であっても R を付けるときは、金属の型を削るだけなので、修正が簡単。
という加工工程としても、後から修正するほうが「安全に倒れる」という興味深い話があるので、そのあたり支点の移動とか応力の分散とかの話に繋げたかったというのがあるわけで。
このあたり、物理屋さんとしては、
- 思考実験をして仮説を出す
- 仮説を確認/証明するために実際の実験をする
- 実験が仮説と違っていたら、仮説を疑う(物理法則は変わらない)
を繰り返す。
これはプログラムのバグ取りとか性能検証とかも同じで、ある程度仮説出して進める。実測データがいくつか取れるが、それが仮説とあっているか検証する。たまに仮説とあっていない場合(思うように性能があがらないとか、本来のバグとは違った箇所を直しているとか)があるので、無理に仮説に合わせようとしないで、一度保留にして仮説に立ち返る、というループになる、という話,
を忘れがちになるので忘備録としてメモしておく。